Lentil convexity

Author’s note. I mean no slight on people who buy tinned lentils. Personally, I quite like them.

The Jolly Contrarian’s Glossary The snippy guide to financial services lingo.™ →Go uptown Out of my cold dead hands. Index — Click the ᐅ to expand: Glossary Tell me more Sign up for our newsletter — or just get in touch: for ½ a weekly 🍺 you get to consult JC. Ask about it here.

So it turns out we haven’t been panic hoarding lentils after all. There is a benign explanation for the sudden disappearance of split peas from the nation’s grocery shelves.

And it is all to do with what happens when apparently harmless normal distributions, like those which seem to govern the purchase of lentils, reveal themselves not to be normal after all. Suddenly, when you are so many standard deviations from the mean that probability theory tells you the risk is as good as zero, the elegant symmetry of the bell curve goes to hell. We’re talking about fat tails.

Lentils in peacetime

In ordinary times, our lentil-buying habits are regular: hippies and vegans buy a lot of lentils, and everyone else buys none. Okay, almost none. The person on the Clapham Omnibus might have one tin, at the back of the cupboard, that someone got in a weak moment years ago, just in case of unexpected apocalypse or visit from long-lost, vegan, cousin from Australia.

But the peacetime lentil-buying motivations of a hippy, a vegetarian and the proverbial meat-and-potatoes munching, Clapham omnibus-riding ordinary fellow are quite distinct, and unrelated. Each person’s decisions are, within a fairly tight range, predictable and and independent of each other: my lentil acquisition does not greatly influence, and is not particularly correlated with, yours.

National weekly lentil purchases therefore usually cleave to a normal distribution. A small part of the population (say 0.5% — the hippies) may buy 8, 9 or 10 tins. A larger part (say 4.5% — vegans, health-food fanatics etc.) may buy one or two, and the remaining 95% will buy very few (let’s say on average 0.1 tin each: one tin between ten, which is probably generous). Since lentil buyers’ decisions are unconnected — that each lentil tin acquisition is an independent event — it all tends to even out, within a range. Each of these numbers will fluctuate, week to week, but in the same week that your hippie stocks up extra for his bom shankar summer solstice druid’s convention cauldron partay, your vegan might skip a tin, and your 95% who hardly ever buy lentils make little difference to the acquisition rate in any weather.

The odds of everyone, including the normals, all going large on lentils in the same week is extremely low. The consequence, across the community, is a normal distribution of weekly lentil acquisition. The random variation in purchases by people in the different demographic groups will cause a small fluctuation in in demand for lentils from week to week, but from a grocer’ perspective, the demand curve is predictable and manageable.

Lentil buying decisions are not independent

Lentil buying projections in peacetime yesterday. The average per 100 people is 15, and any more than 28 is genuinely unthinkable.

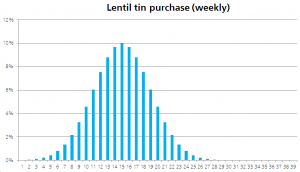
But in actual fact lentil purchasing decisions are not independent, as our new friend the coronavirus pandemic illustrates. They just seem like it, in most markets. Ninety-five percent of the sample are connected by a general disposition not to buy lentils. But this disposition is a function of one’s apprehension of the proximity of apocalypse. Apocalypses are, in the main, rare, and one does not tend to form an opinion that one is nigh purely through ones’ own deductions from meteorological and astronomical data. Rather, we apprehend oblivion because someone said it on Twitter. Because Owen Jones wrote a thought-piece on it, or because — by Jupiter, everyone is suddenly buying lentils and there are hardly any left in Sainsbury’s.

So, we get infected with the idea of Apocalypse by each other. Our legume-buying habits are not independent after all. They are all formed out of a collective consensus about the non-imminence of the second coming. While each person’s threshold for precautionary lentil purchase in the event of imminent apocalypse will differ, across the group, news of the unchecked spread of coronavirus will bring each person closer to that threshold, and will push some of them over it.

As they walk past the tinned goods shelf, it only takes a small proportion of that 95% to pick up a tin to blow the grocer's expectations out the window. Let’s say 5 of the 95% decide to buy an extra single tin each. As the hippies vegans and health nuts, who buy lentils for fun, are also buying their regular quota, we can see that in nervous times, the supply of lentils will diminish quickly.

And now a second order of dependence emerges. For some of the 95%, who have not yet crossed the the threshold for precautionary lentil purchase, notice that the lentil shelf in the supermarket is nearly empty. It prompts them to reconsider their apprehension of apocalypse. They move closer to their threshold. They collect the remaining lentils.

The supermarket management will now intervene, alarmed at this sudden run on lentils. Their immediate reaction will be to impose an item limit. It posts a sign on the shelf restricting customers to 3 tins each. Limiting most customers, who would normally be seen dead buying one tin, to three, has no effect on the problem, since our lentils-for-judgment-day-only types, would have bought one tin anyway: the problem is not that one or two people are bulk buying, but that all people are single-item buying. The three-items per customer (a) irritates the hippies who would ordinarily buy ten tins anyway, and (b) further validates the suspicion among non-hippies that we are indeed in desperate times. After all, one could hardly ask for a clearer sign of of imminent Armageddon than LENTIL RATIONING — I mean, panic buying hippy food: could it get any worse than that? The 95%, one one, up their demand from one tin to the maximum permissible three.

The fat tail of the distribution overlaid. In ordinary times, in the middle of the bell, the distributions look the same, but the tails are different. There is a material chance of demand a long way down the tail

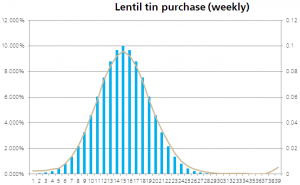
Still: no panic hoarding, but the shelf is bare. And those latecomers, discovering it is now too late to stock up on lentils, head to borlotti beans and Mexican bean fiesta. To their horror they discover these have been cleaned out as well.

Every distant fear about a forthcoming final reckoning now confirmed, they stampede for the couscous and quinoa.

Implications

The interconnectedness between human decisions like lentil-buying is not stable. You can’t model it. You can’t predict it. The correlation changes on account of the very existence of each buying decision, and each other people’s reaction to that decision. For the most part, one person’s buying decision won’t affect another’s. The decisions look for all the world as it they are independent. Near to the mean the chart looks a lot like a bell curve. Hence, for most of the time, the bell curve works well enough. But events which are really independent stay independent, however weird things get. The odds of flipping heads on a fair coin stays 0.5 however often you flip it, and whatever the previous results. This makes the job of modelling independent events much, much easier. In fact it makes it possible. Modelling dependent events isn’t just a case of more complex maths. It isn’t possible.

See also

• Fat tail