Lentil convexity

The Jolly Contrarian’s Glossary The snippy guide to financial services lingo.™ →Go uptown Out of my cold dead hands. Index — Click the ᐅ to expand: Glossary Tell me more Sign up for our newsletter — or just get in touch: for ½ a weekly 🍺 you get to consult JC. Ask about it here.

Author’s note. I mean no slight on people who buy tinned lentils. Personally, I quite like them.

So it turns out we haven’t been panic hoarding lentils after all. There is a benign explanation for the sudden disappearance of split peas from the nation’s grocery shelves.

And it is all to do with what happens when apparently harmless normal distributions, like those governing the purchase of lentils, reveal themselves not to be sp normal after all. Suddenly, when you are so many standard deviations from the mean that probability theory tells you the risk is as good as zero, the elegant symmetry of the bell curve goes to hell. We’re talking about fat tails.

Lentils in peacetime

In ordinary times, our lentil-buying habits are regular: hippies and vegans buy a lot of lentils, and everyone else buys none. Okay, almost none. The person on the Clapham Omnibus might have one tin, at the back of the cupboard, that someone got in a weak moment years ago, just in case of unexpected apocalypse or visit from long-lost, vegan, cousin from Australia.

But the peacetime lentil-buying motivations within the community are unrelated. Overall appetite is, within a tight range, predictable. The lentil-acquiring proclivities of each individual are independent: that is to say, my lentil acquisition does not greatly influence, and is not especially swayed by, yours.

National weekly lentil purchases therefore usually cleave to a normal distribution. A small part of the population (say 0.5% — the hippies) may buy 8, 9 or 10 tins. A slightly bigger section (say 4.5% — vegans, health-food fanatics etc.) may buy one or two, and the remaining 95% will buy very few (let’s say on average 0.1 tin each: one tin between ten, which is probably generous). Since these lentil buyers’ decisions are independent events — it all tends to even out, within a range. Weekly overall tin purchases will fluctuate but overall the individuals will tend to even each other out. In the same week that your hippie stocks up for his bom shankar summer solstice druid’s convention cauldron partay, a vegan might skip a tin, and your 95% who hardly ever buy lentils make little difference to the acquisition rate in any weather.

Lentil buying projections in peacetime yesterday. The average per 100 people is 15, and any more than 28 is genuinely unthinkable.

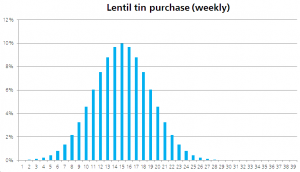
The odds of everyone, including the normals, all going large on lentils in the same week is extremely low. The consequence, across the community, is a normal distribution of weekly lentil acquisition. The random variation in purchases by people in the different demographic groups will cause a small fluctuation in in demand for lentils from week to week, but from a grocer’ perspective, the demand curve is predictable and manageable.

Lentil buying decisions are not independent

But in actual fact lentil purchasing decisions are not independent, as our new friend the coronavirus pandemic illustrates. They just seem like it, in most markets. Ninety-five per cent of the sample are connected by a general disposition not to buy lentils. But this disposition is a function of one’s apprehension of the proximity of apocalypse. Apocalypses are, in the main, rare, and one does not tend to form an opinion that one is nigh purely through ones’ own deductions from meteorological and astronomical data. Rather, we apprehend oblivion because someone said it on Twitter. Because Owen Jones wrote a thought-piece on it, or because — by Jupiter, everyone is suddenly buying lentils and there are hardly any left in Sainsbury’s.

So, we get infected with the idea of Apocalypse by each other. Our legume-buying habits are not independent after all. They are all formed out of a collective consensus about the non-imminence of the second coming. While each person’s threshold for precautionary lentil purchase in the event of apocalypse will differ, across the group, news of the unchecked spread of coronavirus will bring each person closer to that threshold and will push some of them over it.

Back to the 95% normals. As they walk past the tinned goods shelf, it only takes a small proportion of that 95% to decide this is the week to pick up an extra tin to blow the grocer's expectations out the window. Let’s say, unnerved by all this elbow-touching and hand-washing carry one, just 5 of the 95% decide to buy an extra tin. As the hippies vegans and health nuts who buy lentils for fun are also buying their regular quota, in these nervous times the supermarket’s lentil supply quickly diminishes.

Then an unexpected second order of dependence emerges. For some of the 95%, who have not yet crossed the threshold for precautionary lentil purchase, notice that the lentil shelf is nearly empty. They reconsider their apprehension of the apocalypse. They move closer to their threshold. Some cross it. They collect a tin each. The shelf is cleaned out.

The supermarket management, alarmed at this inexplicable sudden run on lentils, will now intervene. They impose a 3-item limit for each customer. But limiting most customers, who would not normally be seen dead buying one tin of lentils, to three, won’t help the problem, since the lentils-for-judgement-day-only contingent only wanted one tin each in the first place. The problem is not these people bulk buying, but that all of them are single-item buying. It will also irritate those hippies and rabbit-food munchers who would ordinarily buy more tins than that even when they weren’t panicking.

Not only will it not help, but(b) further validates the suspicion among the 95% non-hippies that we are indeed in desperate times. After all, one could hardly ask for a clearer sign of of imminent Armageddon than LENTIL RATIONING — could things get any more desperate?

The 95%, as one, increase their demand to the maximum permitted. It is only common sense.

The fat tail of the distribution. In the middle of the “bell”, the distributions look quite similar. At the extremes they are very different.

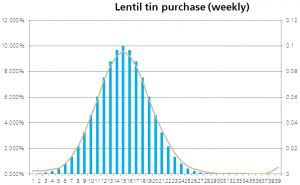
Still: no panic hoarding, but the shelf is bare. And those latecomers, discovering it is now too late to buy lentils, head to borlotti beans and Mexican bean fiesta. To their horror they discover these have been cleaned out as well. Every distant fear about a forthcoming final reckoning now confirmed, they stampede for the couscous and quinoa.

Implications

We can see the interconnectedness between human decisions like lentil-buying, at the extremes is not stable. You can’t model it. You can’t predict it. The correlation changes on account of the very existence of each buying decision, and each other people’s reaction to that decision. In ordinary times one person’s buying decision won’t affect another’s. They look for all the world like truly independent events. What do I care whether you bought lentils? But events which are really independent stay independent, however weird things get. The odds of flipping heads on a fair coin stays 0.5 however often you flip it, and whatever the previous results. This makes the job of modelling independent events much, much easier. In fact it makes it possible. Modelling dependent events isn’t just a case of more complex maths. It isn’t possible.

See also

• Fat tail