Finite and Infinite Games
|
|
PUBLIC SERVICE ANNOUNCEMENT
If there is one thing to take from this article, please make it this: read James P. Carse’s magnificent Finite and Infinite Games: A Vision of Life as Play and Possibility and not Simon Sinek’s hasty adaptation, The Infinite Game.
Thank you. Normal programming continues below.
“It wasn’t infinity in fact. Infinity itself looks flat and uninteresting. Looking up into the night sky is looking into infinity — distance is incomprehensible and therefore meaningless. The chamber into which the aircar emerged was anything but infinite, it was just very very very big, so big that it gave the impression of infinity far better than infinity itself.”
James P. Carse was a Professor of the History and Literature of Religion at NYU for thirty years. In that time, he garnered little great acclaim — his Wikipedia page is perfunctory — publishing a handful of monographs that have had little lasting impact. He earns this lengthy encomium thanks to his one great exception to that record: 1986’s Finite and Infinite Games: A Vision of Life as Play and Possibility, a short book which, though thickly camouflaged, is an absolute monster.
It, too, might have silted mutely into the geological record, somewhere between Julian Jaynes and Francis Fukuyama, were it not for that great populariser of turgid commonplaces Simon Sinek who stumbled across it, signally misunderstood it and then wrote a quite wretched pop psychology book with a similar title mangling what he took to be Carse’s general theme.[1]
Though Sinek’s book is a truly terrible misreading, he has at least popularised Carse’s original — I for one would not have heard of it otherwise — so we can be at least grateful to the great TED talker for that.
Carse, who died in 2020, wrote with an affected aphoristic style, so is not an easy read. He was in the habit of saying things like:
“… if you are the genius of what you say to me, I am the genius of what I hear you say. What you say originally I can hear only originally. As you surrender the sound on your lips, I surrender the sound in my ear.”
This is not going to be to everyone’s taste. Not everyone will even follow it, as Sinek illustrates. But you do get used to the style — it is “literary” enough to reward re-reading — and Carse’s ideas have a habit of percolating even after you have put the book down. They sometimes come back days or weeks later. This is the sign of a special work. When individuals as luminous as Stewart Brand speak reverently of it, there might be life for it yet above the daisies.
I hope so. Here is my go at keeping it above ground.
What are “finite” and “infinite” games?
Carse’s central idea is that much if life is comprised of two types of “game”: zero-sum competitions that we play to win, and unbounded collaborative games, that we play to continue playing.
A finite game is, in the narrow sense, a contest: fixed rules, fixed boundaries in time and space, an agreed objective and, usually, a winner and a loser. For example, a football game, boxing match, a dog-fight or a board game.Notably, both Chess and Go are finite games. Litigation is perhaps the perfect, idealised finite game.
An infinite game has no fixed rules, boundaries, or teams; participants can agree change rules or roles as they see fit, to help play to continue. For example, a market, a community, a business, a team or a scientific paradigm. Compared with finite contest, infinite games are (Q.E.D.) nebulous arrangements but one thing is clear: there are no winners and losers. The idea is to avoid a final result. Everyone plays to keep playing, and keep others playing. A commercial negotiation is the idealised infinite game.
Finite games are from Mars, via Thomas Hobbes and a team of litigators.
Infinite games are from Venus, via Adam Smith and his team of salespeople and structurers.
Exclusive and inclusive
Their very nebulousness means infinite games are inclusive, and you can play many of them at the same time. We all do, with our careers, families, friendships, communities and social groups. Their boundaries being both fluid and porous, these infinite games permeate, elide, intersect, interlock and amalgamate, and as they do a skilled player adjusts her play.
Finite games tend to be exclusive: once you are in one, it dominates whatever else you could otherwise be doing: it is — at least symbolically — a fight to the death, so you can be forgiven for being preoccupied. Since you know where you may go, what you may do, and when it must end, it is possible to sacrifice whatever other interests you may have had while you play the finite game.
Infinite game being naturally fluid, they can wrap around a finite game, but not vice versa.
Not to be confused
In any case, it is important in life to know when you are playing a finite game, and when you are involved in infinite play, and not to confuse them.
The thrust of Simon Sinek’s book is that in much of modern life we do confuse them: that when we carry over the “finite” metaphors of sport and war into business and politics, and play infinite games to win them, we make a category error.
But the distinction is subtler than it at first appears. A football match is finite; a football team is infinite. The team plays each match to defeat its opponent utterly. But in a broader sense, every football team needs opponents, and not just so it has someone to wallop every Saturday. It is important for the team’s future that it could realistically lose — indeed that, on occasion, it does lose — so that the games it plays offer the realistic prospect of “drama” (and not merely “theatrics”).
While a football team never wishes to lose any particular match — each is a finite game — in the long run it must lose some matches in general, lest spectators and players get bored. This is an infinite game. No-one wants to be beaten every time. No-one wants to win every time. No-one wants to watch a foregone conclusion. Ergo, we play finite games in the context of a broader infinite game.
The finite versus the infinite
Carse spends much of Finite and Infinite Games (unfavourably) comparing finite with infinite play. If much of what we tend to see as an existential struggle need not be anything of the kind, it is worth understanding these structural differences.
They have strong resonances with some of the JC’s other favourite big, odd ideas.
“Historic” versus “prospective”
The criteria for a finite game — agreed rules, formal boundaries and a limited period for one side to prevail over the other — means they are “historic” in nature. Even as you play them, you proceed by reference to risk — calculable probabilities for a known set of possible outcomes — and not uncertainty — unknown, or unknowable outcomes.[2]
The result of a football game is only certain at the end, and is a function of what happened. What could have happened but did not, and what might happen in the future, if things were only different, is of no concern to anyone playing a finite game.
Side-bar for legal eagles: the common law — based as it is on the doctrine of precedent; you know, “what has been decided before” — is dispositionally historic. Until it isn’t. For what are the great cases, the law reports and textbooks if they are not a catalogue of all the times the courts made something new?
By contrast, infinite games, where the object is to find a way to carry on, care little about what has already happened, other to learn from the experience do more of what worked and less of what didn’t. What’s done is done. The challenge is figuring out what’s coming next. This is necessarily prospective. Infinite games harness knowledge and experience to look forward.
Theatrical and dramatic
Carse describes historical, close-ended games as “theatrical,” in the sense that they run on pre-laid rails and can only have results from a range of outcomes that have been determined in advance. This, he contrasts with real “drama”, where by avoiding outcomes, players must improvise to keep the future open. There may be some drama in a finite game — we may not know who will win the World Cup — but that drama is only provisional, since it will ultimately be resolved in an expected, probabilistic way: we do know that one team will win, and 31 will not.
Now, historically-focused finite games are fine, if that’s what floats your boat: there is no harm and much reward to be had from football, as long as everyone understands the “theatricality” of what’s going on. But to use backward-looking techniques to resolve forward-looking, indeterminate scenarios — to treat the future as a calculable risk rather than an unknowable uncertainty — is to make a category error.
This is what business thought-leaders who use sports metaphors do.
The Global Financial Crisis and the lives of the universe
“We were seeing things that were 25 standard deviation moves, several days in a row”.[3]
Like the common law, markets are dispositionally historic until they aren’t. Finite techniques work well enough, much of the time, because infinite environments can resemble finite games, much of the time.
In “ordinary market conditions”, commerce does seem to operate according to an established order, existing conventions and what is already known. Rules feel fixed. Competition is apparent. Institutions are profitable, market titans are powerful — if not necessarily “strong” — the crowd is wise and everything runs as if impelled by an invisible hand. Until it doesn’t.
Why do we prefer finite, historical, backward-looking techniques over forms of infinite play? Because they are cheaper to implement and easier to manage. As long as the environment is predictable, a “historic” approach delivers efficiency, consistency and certainty. Executives can exercise central control as if they were playing a finite game. They can manage by algorithm. They can use dependable machines, and dispense with unreliable meatware. They can scale, and their risks and returns scale proportionately. This is why they are so fond of sporting metaphors.
When the assumption of finitude breaks down — when normal and fat-tailed distributions diverge — scale becomes a monster. Just ask David Viniar, or Myron Scholes, or John Meriwether, or Dick Fuld, or the prime brokers to Archegos.
Suddenly, probability metaphors fail. One twenty-five standard-deviation move is preposterous. You would not expect one in several trillion, trillion lives of the universe, let alone “several days in a row”.[4]
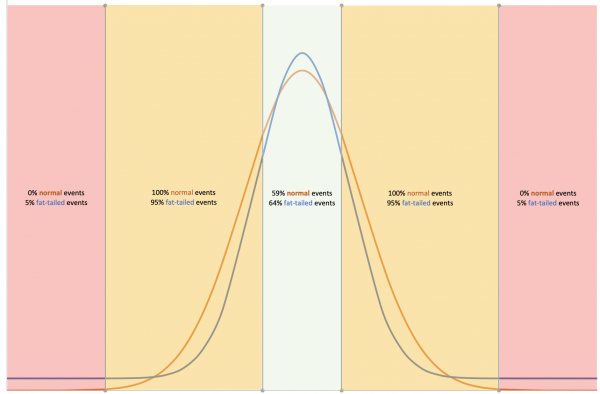
Finite games are concerned with risk. Infinite ones are concerned with uncertainty. But risk and uncertainty are hard to tell apart in normal times. For the parts of a normal distribution that roughly resemble a “fat-tailed” distribution — most of it — historical approaches will work passably well for both, as long as the events fall within the middle, which for the most part they do.
Power and strength
“A powerful person is one who brings the past to an outcome, settling all its unresolved issues. A strong person is one who carries the past into the future, showing that none of its issues is capable of resolution. Power is concerned with what has already happened; strength with what has yet to happen. Power is finite in amount, strength cannot be measured because it is an opening and not a closing act. Power refers to the freedom persons have within limits, strength to the freedoms persons have with limits.
Power will always be restricted to a relatively small number of selected persons. Anyone can be strong.”It is fashionable in our time to speak loosely about “power” — much of critical theory resolves a manifesto against the violence power structures do to the marginalised — and Carse’s distinction between “power” and “strength” is a good reminder to exercise care here.
Sure, social organisations can be pernicious, but most are not. Families are power structures. So are local communities. Cricket clubs. Parent-teacher associations. Critical theories themselves are paradigms — social hierarchies of just this kind. Any form of communal organisation more developed than flapping around in primordial sludge involves some compromise of interests and some hierarchy. These don’t have to be destructive: they can be constructive, enabling, levers to prosperity and betterment for everyone who wants it. If we call such a centralised, curated, defended store of knowledge for sharing a “strength structure” it does not sound so ominous.
Society and culture: awards versus potential
Carse distinguishes between “society” — historical, bounded — and culture” — a provisional alignment of values primed for onward progress. He may have described a power structure as of “society” and a “strength structure” as of “culture”. The historic, zero-sum nature of finite games contrasts with the prospective, permissive nature of infinite ones.
Society is finite, bounded, and patriotic: it functions in order to establish a hierarchy, bestowing status, titles, honorifics and awards based on what has already happened. These emblems of past victories and achievements grant certain participants formal status. They are markers of acquired power (and not potential strength). Those with such status are impelled to defend and reinforce the hierarchy because they are have done well in it. One desires the permanence of society because it vouches safe the permanence of one’s titles and prizes.
Culture is infinite, unbounded, endlessly creative and sees its history not as destiny, but tradition: a narrative that has been started but is yet to be completed and that may be adjusted as required. That said, culture is a deep layer: it has mass and momentum, and will not change quickly, but it does change over time.[5]
Top-down versus bottom-up
In the same way finite games are backward-looking and not prospective, they imply centralised over distributed decision-making. The ingenuity is in the middle — or, in a hierarchy, at the top — and those at the edges are just there to carry out instructions.
Thus, football managers formulate strategy and recruit players best able to execute it, drilling them with pre-formulated tactics, plays and set-pieces. Indeed, managers are so important that they are not allowed to intervene during the match and must delegate that role to an on-field captain who directs operations as the game unfolds. Under these circumstances, a well-coached team of ordinary players may prevail over a disorganised assembly of better athletes. This is the lesson of Michael Lewis’ Moneyball: The Art of Winning an Unfair Game, and the falsification of the “Galácticos” strategy of buying the best players money can buy, and expecting their virtuosity to prevail.[6]
Elite coaching works because rules are fixed, variables known, and there are tight parameters around what players can do, where they can do it.
Now as far as business is a finite game, there is much to take from this. Out in the field, form dominates substance: the most vital talents are those who formulate rules, work out algorithms, devise playbooks and source — or outsource — the personnel who will faithfully and efficiently follow the plan.
If business is a finite, zero-sum game, there are a few implications:
Firstly, brilliant minds belong at the top of the organisation: they do the most inspired thinking. They come up with the best plan. Securing “the person with the best plan” is worth paying extraordinary amounts of money for.
Secondly, the organisation’s sacred quests are the creation of excellent process and optimising the cost of carrying it out.
Thirdly, those whose job is to put the leadership’s plans into practice must, as far as possible, follow instructions as quickly, flawlessly and cheaply as possible. If your unique selling point is your central strategy, the last thing you want your players to do is improvise. They should act like automatons. In a perfect world, they would be automatons.
Note the drift: for operational staff, it is towards efficiency; for executive administrative staff, it is towards excellence.
But if business is an infinite game, we have a different proposition. The rules aren’t fixed. We can’t predict where the game will go or what other players will do or, for that matter, who’s even playing. There is no common end-goal. A super-coach with a pre-determined strategy is no good. Here you do want Galácticos — only ones with a talent not for closing out historical conflicts, but seeing new possibilities, creating new metaphors, building new narratives.
Carse calls these players “poietai” — a Platonic concept meaning something like “poet” — an unfortunate label if you want to go across with sports-obsessed MBAs — which we might also render as “creatives”.
In any case, infinite players are not competing, but creating.
We want creative players to be virtuosos, and not rule-followers. They must have the freedom and resource to carry on — to augment the game. The coach’s role is to build out a simple, robust and permissive infrastructure that lets creatives communicate, puts tools in their hands, enables them to reallocate resources as they see fit. The coach’s overarching goal should be to empower players to make quick and effective decisions in the field, and otherwise to keep out of the way.
This is quite the opposite model to the super-coach: here the greatest value is provided at the edges of the organisation. The bottom-up model: laissez-faire; invisible hand; evolutionary.
Form and substance
We have argued elsewhere, at tedious length, that the great curse of modernity is the primacy of form over substance.
In finite games that distinction can be trivial; in an infinite game it is not.
In a backward-looking, proven, data-complete universe, substance is simply a specific articulation of form. The universe is solved; there is an exclusive optimal move and it can be derived from first principle. Substance follows from — depends on — form.
Form is an axiom; substance is its articulation with numbers. If you have right equation you will get the right answer. This depends on the universe being bounded, all rules determined, all knowns known. It depends, therefore, on the conditions existing for a finite game.
Where the universe is not bounded, where rules change, where unknowns swamp knowns[7] — where the game is infinite — substance is not a function of form. There are no equations, axioms or formulae to follow when interacting with complex adaptive systems.
It’s all well in theory
This will all take time, patience and persistence
Finite and Infinite Games is a work of abstract principle, not a practical guide to life. Metaphors cannot rid the world of suffering, not resolve the intractable mess that is our world. Our institutions have fashioned themselves over aeons in their own images. They will not change overnight.
We should not expect an over-managed multitude of hide-bound rule-followers to pivot overnight to enlightened, terra-forming creatives. If you spent your career learning how to follow rules, being told suddenly those at the coal face must “be agile” and figure it out as they go will present as some kind of terrifying nightmare — it will be beyond the capacity of customer-facing staff, and it will represent an existential threat to (and be beyond the capacity of) those in upper middle management, who for decades have grown to like the idea that business administration is the highest form of being. The system will be motivated against this shift. It will deftly reorganise itself to resist it.
That is to say, our narratives, for better or worse, are a matter of culture. Culture sits deep in the ontology of a system. It moves slowly. It cannot change overnight.
A third category: interminable games
There is a third type of game that Carse may have overlooked, but which increasingly dominates public discourse, and is a kind of hybrid of the two — or a dark inversion of an infinite game: let’s call them “interminable games”.
Interminable games are destructive where infinite ones are creative. Instead of seeking to create new worlds and open up possibilities, each side seeks to shut the other one’s existing world down. They are mainly harmless — just tiresome — because neither side will ever win.
Does God exist? Is Socialism good? Is Capitalism bad? Are permissionless blockchains the future? Will string theory explain life, the universe and everything? Whither social justice? Is Brexit a success? These are interminable games.
Like finite games, they appear to be contests “to the death”. Yet, like infinite games, they must not be finally resolved. The goal is, always, to avoid final victory and carry on the fight because ,if you win, you have to pack up your banners, disband your army and go home. Therefore, should outright victory impend, likely victors will scramble to change their own terms of reference until they have something else to fight about.
This can work because, the rules of engagement are not fixed, or even agreed: each side is playing to its own rules, with total disregard for the other’s, and will change its premises should it appear to be on the brink of victory or defeat.
No boundaries
All models are wrong. But some are useful. — George E. P. Box
Ultimately, the distinction between finite and infinite games eludes. The games we play are not all well-defined. What looks today to be an infinite game of creative possibility can, tomorrow resemble a fight to the death. As with any model of the world, we should use it to frame and illuminate, not to rule. Finite and Infinite Games is no great falsification of the world as we see it: to treat it that way would be wilfully to misunderstand its essential argument.
Instead, it offers us tools to reimagine ourselves, our struggles, our achievements and the world. The more ways we can redraw ourselves, the better we can play the infinite game.
See also
References
- ↑ Simon Sinek, The Infinite Game (2019)
- ↑ “In a world of risk (“small world”), all alternatives, consequences, and probabilities are known. In uncertain (“large”) worlds, some of this information is unknown or unknowable.” — Kirsten Volz and Gerd Gigerenzer
- ↑ David Viniar, Chief Financial Officer, Goldman Sachs, August 2007.
- ↑ You would expect a “25-sigma move” on one in 1.3 billion billion billion billion billion billion billion billion billion billion billion billion billion billion days, which is several trillion trillion trillion trillion times as long as the life (to date) of the known universe. More on this fascinating topic in our normal distribution article.
- ↑ Stewart Brand’s idea of “pace layering” is another one of the JC’s favourite big, odd ideas. Stay tuned.
- ↑ There are those who doubt the Moneyball story, and those who think the Galácticos largely had it right.
- ↑ All data is from the past. Seeing as there is an infinite amount of data from the future, the portion of the available data we have is, effectively, nil.
