Semantic structure

The JC’s guide to writing nice.™ →Go uptown On what kind of ball may be used with what kind of game A single, branching proposition where the subject is the ball: 1. A ball: (a) if it is red (i) if it is round (A) must not be used for rugby union (B) must not be used for rugby league (C) may be used for test cricket (D) must not be used for one-day cricket (ii) if it is oval: (A) may be used for rugby union (B) may be used for rugby league (C) must not be used for test cricket (D) must not be used for one-day cricket (b) if it is white: (i) if it is round: (A) must not be used for rugby union (B) must not be used for rugby league (C) must not be used for test cricket (D) may be used for one-day cricket (ii) if it is oval: (A) may be used for rugby union (B) may be used for rugby league (C) must not be used for test cricket (D) must not be used for one-day cricket The above, captured Two branching propositions where the subject is the ball: 1. An ball that is oval: (i) may be used for rugby (ii) must not be used for cricket 2. A ball that is round: (i) must not be used for rugby (ii) if it is red: (a) may be used for test cricket (b) must not be used for one-day cricket (iii) if it is white: (a) must not be used for test cricket (b) may be used for one-day cricket Reorganising by ball shape makes two simpler decision trees Three non-branching propositions where the subject is the game. 1. Rugby must be played with a ball that is oval 2. Cricket must be played with a ball that is round and: (i) in test cricket, red (ii) in one-day cricket, white But organising by code, then colour, is simplest of all. Index: Click ᐅ to expand: Plain English Drafting Tell me more Sign up for our newsletter — or just get in touch: for ½ a weekly 🍺 you get to consult JC. Ask about it here.

It is easy to forget is how important is the logical structure of your writing. Not just the paragraph organisation, but the semantic structure underlying the sentences themselves.

Any statement boils down to a logical proposition, and so on. It is like software code, only instead of subroutines, conditions, logic gates, if/then statements, lawyers call them obligations, rights, discretions, provisos, inclusos, options, definition.

For example, an obligation is an if-then statement; option is an either-or gate. Some legal operators like “(whether or not...)”, “(including without limitation...)”, “(for the avoidance of doubt...)”, “(may, but need not...)” do not constrain or expand the propositions they act on and can be omitted from a logic map (just as they should be omitted from the draft, dammit).

Any “logic gate” that splits a proposition into alternatives increases its inherent complicatedness. How you organise your gates, therefore, makes a big difference to how complicated your proposition turns out.

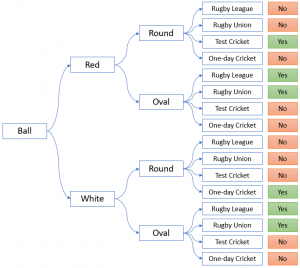
Take the alternative statements about cricket and rugby balls in the panel at right. (For non-initiates, rugby is played with a large oval ball which may be any colour; cricket with a small round ball which (for one-day cricket) must be white and (for test cricket) must be red. In the abstract, the variables at play here are:

• ball shape (round or oval)
• ball colour (red or white (or other))
• code (rugby or cricket)
• code variation, which in turn breaks into
  • cricket: test or one-day (relevant only to cricket)
  • rugby: union or league (relevant only to rugby)

How you arrange these variables can generate a more or less complicated logical structure, depending on how many distinct logic trees you create, and how you order the variables within a given logic tree.

One can (making it up as we go along) formulate a few design principles here:

Distinct logic trees

• Create distinct logic trees: The more distinct logic trees you have, the simpler your overall logic will be, though there is a limit (if each logic tree is a straight line then you don't have any logic at all).
• Make sure they are distinct: Distinct logic trees should not intersect with each other: their terms are mutually exclusive. (Intuitively, we suspect that the downstream logic beyond “cricket” will not intersect with any downstream logic beyond “rugby”).
• Avoid dead-ends: Try to minimise logic trees that end in a “no” as these are dead twigs that carry no legal/semantic content, but clutter up the structure.

Logic gates

• Non-overlapping categories: Look for categories of items (such as “rugby” and “cricket”) that do not overlap and deal with them in separate logic trees. There is no real benefit to designing a single tree to accommodate these as alternatives.
• Postpone logic gates as far as possible: Where a logic gate must happen (that is, a split between sub-categories within a single logic tree), make it happen as late as possible, in order to...
• Avoid duplicating branches: Design each logic tree so that a given logic gate only happens once. (In the top diagram , the logic gate between the four code variations appear four times and the logic gate for ball shape appears twice, while the colour logic gate only once. If your draft is studded with expressions like “holder of a bearer note and/or registered owner of a registered note (as the case may, for the time being, be)” you have put your logic gate in the wrong place.

Definitions

Definitions can function as distinct mini-trees: On that note: a definition can act as a mini-logic tree if it contains a logic gate. For example, creating a definition like “Noteholder” means the holder of a bearer note and/or registered owner of a registered note (as the case may, for the time being, be) you can simplify the inherent logic of your text: the more the logic gate appears, the more economy a definition can bring.

Again, there is a tension: creating a definition that you only use once or twice can make comprehension harder. And sometimes by getting rid of the “duplicate gates” problem a definition obscured the fact that the logic was designed badly in the first place.

If you want to create a single proposition that covers all these variables, you commit yourself to a lot downstream branching, because that our single logical structure must accommodate all the permutations.

Therefore, if you frame your logic around first the colour of the ball then its shape, you buy yourself a number of branches which get to “NO” answers, and are therefore useless. See the first figure on the right. The colour of the ball doesn't matter for rugby, so you should postpone that branch until colour does matter for all the remaining branches. that is, after you have got to “cricket”.

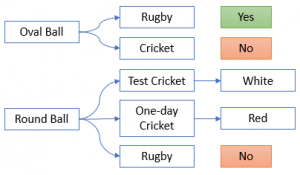
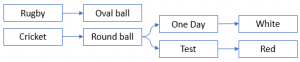
The subject of the sentence and sequence of the branches makes a difference. For example, focussing on the ball first then its colour then its shape, and articulating these by reference to the games, commits to sixteen branches. If we break the proposition into two and focus first on shape, we can reduce this to five. if we reframe the proposition to focus on the game, we can get it down to the three, which is the minimum.

There is doubtless some information theory that optimises the logical structure, but intuitively it seems to us common options should be delayed as far as possible, and where games are largely common, separating out the points where they differ into a separate set of propositions may help.