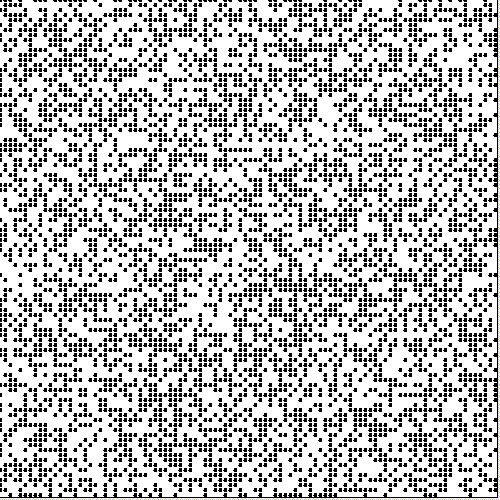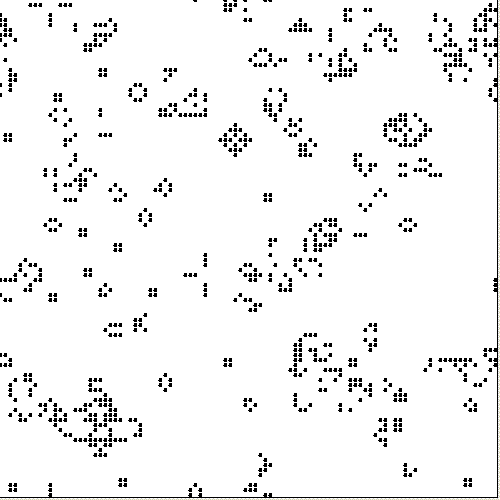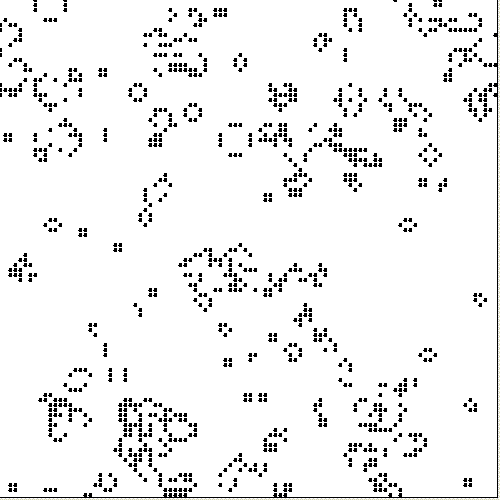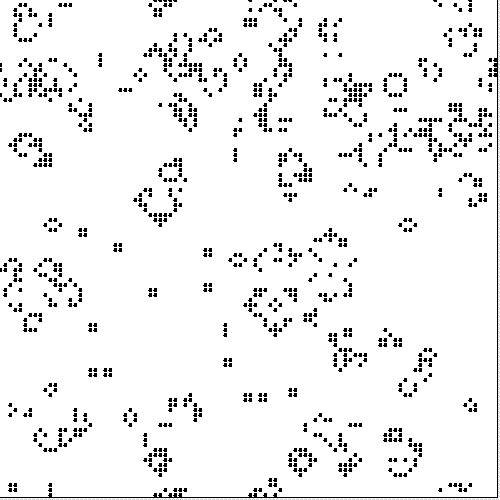Conway’s Game of Life
|
The JC’s amateur guide to systems theory™
|
The “Game of Life” is a cellular automaton — not really a game in a meaningful sense, since it plays by itself — invented by mathematician John Conway in 1970.
It is a simple Turing Machine. It comprises an unbounded, two-dimensional grid of cells, each of which may be “live” (black) or “dead” (white). At each generation every cell interacts with its eight adjacent “neighbour” cells, as follows:
- A live cell with two or three live neighbours stays live.
- A dead cell with three live neighbours becomes live.
- All other live cells die.
- All other dead cells stay dead.
One interacts with the Game of Life by simply creating the initial configuration. Thereafter, one simply watches as it evolves following this simple algorithm. Each generation is a pure function of the preceding one. The rules continue to be applied repeatedly to create further generations.
If you let it go for long enough, or start with an interesting enough configuration, you start to get some quite impressive, and quite unexpected, patterns. This has led computer scientists, evolutionary biologists and like-minded reductionists to rejoice with a premature hosanna for it may illustrate, they feel, how intelligent life could evolve without assistance through simple cellular regeneration.
Premature, because people have been running Conway models more or less continuously since 1970. None have yet deduced rice pudding or income tax, let alone achieved self-awareness.
However you look at it, Conway’s game is by definition mechanical and deterministic. If you run it forward from the same place, it will always yield the same outcome. If you then run it backwards, you will get back to the original configuration. By its own terms there is no way to interfere with its operation, and you cannot change the rules.
In this regard it is a simple system.
Reductio ad absurdum
The JC has encountered reductionists who see complexity as an emergent property of even a simple algorithm of Turing Machine.
On this view, fractals, polynomial mapping, even something as simple as Conway’s Game of Life is, if you let it go long enough, complex, as it spawns sub-systems, gliders, glider guns, and these interact with each other in marvellous and unpredictable ways. There is a tacit assumption here that real life — you know, the offworld — is really just a scaled-up version of the Game of Life, itself being just an implementation of Darwin’s Dangerous Idea, after all.
This is reductionism, only viewed from the wrong end of the telescope. Rather than taking the rich tapestry of modern life and boiling it down to basic rules of cause and effect, as reductionists normally do, this gambit starts with those basic rules, and scales them up. What prevents us from getting from one end of this spectrum to the other, say the reductionists, is only an absence of sufficient data to reverse engineer the algorithm (from the rich tapestry end) and a want of processing power to generate modern life (from the basic algorithm end). The universe is nonetheless fully determined at all levels of abstraction.
Hmm. So however long you run Conway’s life game, it does not seem to arrive at rice pudding and income tax. Reductionists say “Ah, but that is just because the rules aren’t quite right, or we haven’t quite got the right initial configuration”. But then, they would say that.
Complexity as an emergent property of algorithm?
The idea that complexity is merely an emergent probability of a simple algorithm is quite the piece of eliminative reductionism. Eliminative in that it eliminates complexity as discrete state. It converts all complex systems to no more than insufficiently-mapped, not-yet-properly-understood simple systems.
This is like saying — maybe it is saying — an analog signal is no more than an insufficiently granular digital signal. That binary code isn't just a neat way of representing the (apparently richer and subtler) analog universe but that, if you dig deep enough, analog signal reduces to binary code. That binary code is all there is.
If this is right — Spartan if, that — it has deep implications. For it means when we model the universe in binary code we are not just placing a convenient, subjective, all-too-human narrative on a hubbub of white noise — telling ourselves imaginative stories designed to help us get by, but whose “truth” value is beside the point — but that we are getting somehow converging upon the fundamental, transcendent essence of the universe.
Remember, we are so far away from having enough data, information and processing capacity as for the practical difference between these dispositions to be, for all time, nil — but the theoretical distinction between them is fundamental nonetheless.
In both cases, complex systems present us with unpredictable, non-linear outcomes in edge cases. All that differs is why they appear that way. (One is “because they are”, the other “because we have no way to better calculate them”.
But in the first case, any heuristic that helps us make sense of the system ISAs good as any other. There is no “epistemic priority” between competing heuristics: all that matters is what works best, judged by whatever criteria you happen to bring to the table. Beauty is in the eye of the beholder. In the other, there is such an epistemic priority. The most granular binary code is the closest to the truth. This gives the holders of that view grounds for insisting it is preferred, by everyone, over every other heuristic.
If algorithms are complex, everything is complex — or nothing is
Conflating simple algorithms with complex systems undermines the explanatory power of complexity theory. The distinction between simple, complicated and complex systems is meaningful. They are now just points along a continuum, without hard boundaries between them. It is really just saying, “well, in this complex system, something will happen; we don’t know what, but as and when it does we will be able to rationalise it as a function of our rules, by deducing what the missing data must have been.”
Ex-post facto rationalisation to comply with your rules is rather like the work normal scientists do in a research programme, of course. It is a form of narratisation.