Finite and Infinite Games: Difference between revisions
Amwelladmin (talk | contribs) No edit summary |
Amwelladmin (talk | contribs) No edit summary |
||
| Line 38: | Line 38: | ||
===“Historic” versus “prospective”=== | ===“Historic” versus “prospective”=== | ||
Many distinctions between finite and infinite games boil down to their historical perspective: those that look backwards, concerning themselves with what has already been established and laid down — as agreed rules, formal boundaries and limited time periods for resolution necessarily do — will tend to be finite in nature; those that are open-ended, forward looking, and indeterminate — concerned with what has yet to happen, and is necessarily unknown, are infinite. | Many distinctions between finite and infinite games boil down to their historical perspective: those that look backwards, concerning themselves with what has already been established and laid down — as agreed rules, formal boundaries and limited time periods for resolution necessarily do — will tend to be finite in nature; those that are open-ended, forward looking, and indeterminate — concerned with what has yet to happen, and is necessarily unknown, are infinite. | ||
Let me throw in some original research here: historically-focused games are fine: there is no harm and much reward to be had from a game of football as long as everyone understands the “theatricality” of what is going on; but to apply finite, backward-looking techniques to the “resolution” of ''infinite'' scenarios — necessarily forward-looking, indeterminate problems | Let me throw in some original research here: historically-focused games are ''fine'': there is no harm and much reward to be had from a game of football, as long as everyone understands the “theatricality” of what is going on; but to apply finite, backward-looking techniques to the “resolution” of ''infinite'' scenarios — necessarily forward-looking, indeterminate problems (in that you don’t even know that there is a problem, let alone what it is) is where you will get into bother. | ||
It is deceptive in that finite techniques may work perfectly well much of the time, because even infinite environments largely function by reference to established order, existing rules and what is already known — it’s just that they don’t have to, and are liable to change without notice. As long as they behave themselves, a finite approach is efficient, effective, centrally controllable and provides consistency and certainty. This is why unimaginative business leaders are so fond of sporting metaphors. | [[File:Normal vs fat-tailed distribution.png|250px|thumb|right|The ostensible similarity between normal and fat-tailed distributions, yesterday.]]It is deceptive in that finite techniques may work perfectly well much of the time, because even infinite environments largely function by reference to established order, existing rules and what is already known: they look, for the most part, like finite games — it’s just that they don’t have to, and are liable to change without notice. As long as they behave themselves, a finite approach is efficient, effective, centrally controllable and provides consistency and certainty. This is why unimaginative business leaders are so fond of sporting metaphors. | ||
This, we think, is just an other way of noting that the middle of a [[normal distribution]] resembles the middle of a “fat-tailed” distribution and the same approaches will work passably well for both, as long as the events fall within the middle, which for the most part they do. | This, we think, is just an other way of noting that the middle of a [[normal distribution]] resembles the middle of a “fat-tailed” distribution and the same approaches will work passably well for both, as long as the events fall within the middle, which for the most part they do. | ||
Revision as of 11:52, 2 April 2022
|
Finite and Infinite Games: A Vision of Life as Play and Possibility by James P. Carse
|
There is so much in this book. Ostensibly, it is an obscure piece of cod philosophy from a religious studies professor in the mid nineteen-eighties. It might well have silted into the geological record as nothing more than that, but it is having a fertile third age: it has been picked up by life-coach to the LinkedIn generation, Simon Sinek, and when minds as luminous as Stewart Brand’s speak reverently of it, it may have life above the daisies for a little while yet. Hope so.
The central idea is to divide life into two types of games: finite ones, which are zero-sum competitions played with the intention of winning, and infinite ones, played with the intention of continuing to play.
Finite games have fixed rules, fixed boundaries in time and space and an agreed objective — usually to beat the other players. Infinite games have no fixed rules, no fixed boundaries, no fixed teams, and players are free to change the rules if that will help play to continue.
It is important, in life, not to confuse the two. The thrust of Sinek’s book is to insist that much of modern life does: that when we carry over metaphors from sport and war — the quintessential finite games — and apply them to business and politics we make a profound error. This observation is appealing, and intuitively right, but there is much more to Carse’s original thesis than that.
Carse, who died last year, is wilfully aphoristic in his literary style, and this is off-putting.[1] He often says things like:
Of infinite players we can also say that if they play they play freely; if they must play, they cannot play.
Now this is important, but the book would be better — and more scrutable — had Carse taken more time to explain what he means by this. On the other hand, Carse’s theory is fundamentally relativist; he assigns as much of the credit for successful communication to the listener’s imagination as the speaker’s intention, and freely asserts that the two may be different:
The paradox of genius exposes us directly to the dynamic of open reciprocity, for if you are the genius of what you say to me, I am the genius of what I hear you say. What you say originally I can hear only originally. As you surrender the sound on your lips, I surrender the sound in my ear.
This being the case, Carse may have been intentionally gnomic, wilfully leaving room for listeners to make what they will of his mystic runes. This may not be to everyone’s taste — perhaps why Mr. Sinek has been able to make such hay elucidating it.[2] But, irony: the job of imaginatively construing Mr. Carse may have meant by this cryptic aphorisms is a kind of infinite game of its own — one that Mr. Sinek is playing pretty well.
So let us join in.
Carse presents the “finite” versus “infinite” dichotomy through the prism of other dualities, which are interesting in themselves:
Training versus education
“To be prepared against surprise is to be trained. To be prepared for surprise is to be educated.”
We train for finite games, work out moves, have playbooks, solve equations. All being well, players are expected to execute a pre-existing plan, not make up a plan as they go. Preparation is everything. The idea is to eliminate surprise by having, as far as possible, worked them out, and where computing all possible outcomes is not possible, to have computed more possible outcomes than your opponent. This strategy works where all parameters are fixed and all possible outcomes at least knowable in theory — zero-sum games, simple systems — but does not always work in the dancing landscapes of complex adaptive systems. If you prepared for chess, your work will be for naught if the game morphs into draughts — or, more likely in an infinite game, cookery, or music. Here instead of eliminating surprise, you equip yourself to deal with it: you need not answers but tools, heuristics and a facility with metaphor.
Power versus strength
“A powerful person is one who brings the past to an outcome, settling all its unresolved issues. A strong person is one who carries the past into the future, showing that none of its issues is capable of resolution. Power is concerned with what has already happened; strength with what has yet to happen. Power is finite in amount, strength cannot be measured because it is an opening and not a closing act. Power refers to the freedom persons have within limits, strength to the freedoms persons have with limits.
Power will always be restricted to a relatively small number of selected persons. Anyone can be strong.”[3]We speak often about power
Society versus culture
The theatrical versus the dramatic
Inasmuch as a finite game is intended for conclusion, inasmuch as its roles are scripted and performed for an audience, we shall refer to finite play as theatrical. [...]Inasmuch as infinite players avoid any outcome whatsoever, keeping the future open, making all scripts useless, we shall refer to infinite play as dramatic.Dramatically, one chooses to be a mother. Theatrically one takes on the role of mother.[4]
This is a harder distinction to glom, especially since Carse concedes that during a finite game the action is “provisionally” dramatic, since the players write the script as they go along. But the object of the game is to kill the drama by making the outcome inevitable. So provisional, and hostile, to drama.
Poeitas
Original research
There are many resonances here with some of the JC’s other favourite big ideas.
“Historic” versus “prospective”
Many distinctions between finite and infinite games boil down to their historical perspective: those that look backwards, concerning themselves with what has already been established and laid down — as agreed rules, formal boundaries and limited time periods for resolution necessarily do — will tend to be finite in nature; those that are open-ended, forward looking, and indeterminate — concerned with what has yet to happen, and is necessarily unknown, are infinite.
Let me throw in some original research here: historically-focused games are fine: there is no harm and much reward to be had from a game of football, as long as everyone understands the “theatricality” of what is going on; but to apply finite, backward-looking techniques to the “resolution” of infinite scenarios — necessarily forward-looking, indeterminate problems (in that you don’t even know that there is a problem, let alone what it is) is where you will get into bother.
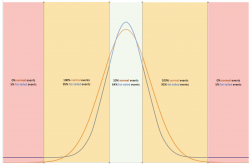
It is deceptive in that finite techniques may work perfectly well much of the time, because even infinite environments largely function by reference to established order, existing rules and what is already known: they look, for the most part, like finite games — it’s just that they don’t have to, and are liable to change without notice. As long as they behave themselves, a finite approach is efficient, effective, centrally controllable and provides consistency and certainty. This is why unimaginative business leaders are so fond of sporting metaphors.
This, we think, is just an other way of noting that the middle of a normal distribution resembles the middle of a “fat-tailed” distribution and the same approaches will work passably well for both, as long as the events fall within the middle, which for the most part they do.
As single-round and iterated prisoner’s dilemmas
A finite game can be part of an infinite game but not vice versa. One could regard a sports franchise an an organisation playing an infinite game through the medium of finite games: here its immediate interests in each distinct match — to comprehensively, theatrically, thrash the opposition — is tempered by its wider interest to keep the infinite game going by creating a compelling sporting contest in which there is the drama that one might not, at any time, win. To carry on that wider, infinite game, one’s opponents must not only survive, but flourish to the point where they can and will beat you in a finite game, thus supplying theatre if not really drama: an unbeatable team is unsatisfying for winners, losers and spectators alike.
And here we wonder a little about the commutability of infinite games into finite ones: sporting matches are like single round prisoner’s dilemmas: zero-sum in a way that recommends only outright domination.
See also
References
- ↑ Notably, Carse’s speaking style is much less cryptic and talks he gavve about the infinite game concept are worth checking out. See for example his talk to the Long Now Foundation: Religious Wars in Light of the Infinite Game.
- ↑ The Infinite Game by Simon Sinek (2019) (see here).
- ↑ Carse, §29.
- ↑ Section 15.