Finite and Infinite Games

The Jolly Contrarian’s book review service™ →Go uptown Index: Click ᐅ to expand: Book reviews Tell me more Sign up for our newsletter — or just get in touch: for ½ a weekly 🍺 you get to consult JC. Ask about it here.

James P. Carse: Finite and Infinite Games: A Vision of Life as Play and Possibility (1986)

There is so much in this book. Ostensibly, it is an obscure piece of cod philosophy from a religious studies professor in the mid nineteen-eighties. It might well have silted into the geological record as nothing more than that, but it is having a fertile third age: it has been picked up by life-coach to the LinkedIn generation, Simon Sinek, and when minds as luminous as Stewart Brand’s speak reverently of it, it may have life above the daisies for a little while yet. Hope so.

The central idea is to divide life into two types of games: finite ones, which are zero-sum competitions played with the intention of winning, and infinite ones, played with the intention of continuing to play. This is to use the expression “game” in conflicting senses; a finite game is one in a narrow sense; an infinite game more like Wittgenstein’s concept of a “language game”.

Finite games have fixed rules, fixed boundaries in time and space and an agreed objective — usually to beat the other players. Infinite games have no fixed rules, no fixed boundaries, no fixed teams, and players are free to change the rules if that will help play to continue.

It is important, in life, not to confuse the two. The thrust of Sinek’s book is to insist that much of modern life does: that when we carry over metaphors from sport and war — the quintessential finite games — and apply them to business and politics we make a profound error: when we take on infinite players in what we take to be a finite game, we bog ourselves down in intractable quagmires: Vladimir Putin, take note. This observation is appealing, and intuitively right, but there is much more to Carse’s original thesis than that.

Carse, who died last year, is wilfully aphoristic in his literary style, and this is off-putting. He often says things like:

Of infinite players we can also say that if they play they play freely; if they must play, they cannot play.

Now this is important, but the book would be better — and more scrutable — had Carse taken more time to explain what he means by this. On the other hand, Carse’s theory is fundamentally relativist; he assigns as much of the credit for successful communication to the listener’s imagination as the speaker’s intention, and freely asserts that the two may be different:

The paradox of genius exposes us directly to the dynamic of open reciprocity, for if you are the genius of what you say to me, I am the genius of what I hear you say. What you say originally I can hear only originally. As you surrender the sound on your lips, I surrender the sound in my ear.

This being the case, Carse may have been intentionally gnomic, wilfully leaving room for listeners to make what they will of his mystic runes. This may not be to everyone’s taste — perhaps why Mr. Sinek has been able to make such hay elucidating it. But, irony: the job of imaginatively construing what Mr. Carse meant by his cryptic aphorisms is a kind of infinite game of its own — one that Mr. Sinek is playing pretty well.

So, let us join in.

Carse presents the “finite” versus “infinite” dichotomy through the prism of other dualities, which are interesting in themselves:

Training versus education

“To be prepared against surprise is to be trained. To be prepared for surprise is to be educated.”

When we play finite games, we train, but do not need education. A tactician works out moves, devises playbooks, and solves equations, presenting all to the players for ingestion and later regurgitation. All being well, by clinical execution, players overcome their opposition. The team that wins is the one that executes most effectively. Players do not make up a plan as they go: their judgment is limited to selecting which part of the plan to execute when, and in response to what. Preparation is everything. The idea is to eliminate surprise by having, as far as possible, worked them out, and where computing all possible outcomes is not possible, to have computed more possible outcomes than your opponent.

This is the modernist, computerised model of operation: fast, perfect calculation. One does not want variability. The last thing you want is a player using her initiative: that can ruin everything.

This strategy works where all parameters are fixed and all possible outcomes at least knowable in theory — zero-sum games, simple systems, football matches — but does not always work in the dancing landscapes of complex adaptive systems. If you prepared for chess, your work will be for naught if the game morphs into draughts — or, just as likely, cookery, music, or electronics. Here, instead of eliminating surprise, you equip yourself to deal with it: you need not answers but tools, heuristics and a facility with metaphor.

Power versus strength

““A powerful person is one who brings the past to an outcome, settling all its unresolved issues. A strong person is one who carries the past into the future, showing that none of its issues is capable of resolution. Power is concerned with what has already happened; strength with what has yet to happen. Power is finite in amount, strength cannot be measured because it is an opening and not a closing act. Power refers to the freedom persons have within limits, strength to the freedoms persons have with limits.

Power will always be restricted to a relatively small number of selected persons. Anyone can be strong.””

It is fashionable to speak loosely about “power” in our time — much of critical theory is a manifesto against the violence power structures do to the marginalised — and Carse’s distinction between “power” and “strength” reminds us to exercise care.

Sure, social hierarchies can be pernicious, where operated by those engaged in a fight to the death, but most people are not. Critical theories themselves are paradigms — social hierarchies of just this kind. Those who who favour any form of communal organisation more developed that flapping around in primordial sludge will concede that social arrangements don’t have to be destructive: they can be constructive, enabling, levers to prosperity and betterment for everyone who wants it. If we call such a centralised, curated, defended store of knowledge for sharing a “strength structure” it does not sound so ominous.

“Strength is paradoxical. I am not strong because I can force others to do what I wish as a result of my play with them, but because I can allow them to do what they wish in the course of my play with them.”

“Society” versus “culture”

“Society they understand as the sum of those relations that are under some form of public constraint, culture as whatever we do with each other by undirected choice. If society is all that a people fells it must do, culture “is the realm of the variable, free, not necessarily universal, of all that cannot lay claim to compulsive authority”.”

Perhaps Carse would describe a power structure as “society” and a strength structure “culture”. The historic, zero-sum nature of finite games contrasts with the prospective, permissive nature of infinite ones.

Society is finite, bounded, and patriotic: functions to establish a hierarchy, bestowing titles, honorifics and awards — the emblems of past victories in combat, and markers of power —to grant certain participants formal status. One desires the permanence of society because it vouches safe the permanence of one’s titles and prizes.

Culture is infinite, unbounded, endlessly creative and sees its history not as destiny, but tradition: a narrative that has been started but is yet to be completed and that may be adjusted as required. Just as one can can play finite games within the context of an infinite one, so can there be society within culture.

The “theatrical” versus the “dramatic”

Inasmuch as a finite game is intended for conclusion, inasmuch as its roles are scripted and performed for an audience, we shall refer to finite play as theatrical. [...]

Inasmuch as infinite players avoid any outcome whatsoever, keeping the future open, making all scripts useless, we shall refer to infinite play as dramatic.

Dramatically, one chooses to be a mother. Theatrically one takes on the role of mother.

This is a harder distinction to glom, especially since Carse concedes that during a finite game the action is “provisionally” dramatic, since the players write the script as they go along. But the object of the game is to kill the drama by making the outcome inevitable. So provisional, and hostile, to drama.

The value of artists

A society that wishes to transcend itself and stay in touch with its culture must embrace its “inventors, makers, artists, story-tellers and mythologists”: not those who deal in historical actualities, but who help imagine new possibilities for how the culture might be.Their mode of engagement having no particular intended outcome or conclusion, they can appear hostile to those already holding rank, title or position in society, and who would rather shore up the historical record to validate their victories.

Society is ambivalent towards the dreamers and malcontents who imagine a different order — they once broke Mick Jagger on a wheel; now he’s a peer of the realm — but they operate not by directly confronting the established order, but by sketching out an imagined alternative which eventually takes root.

Original research

There are many resonances here with some of the JC’s other favourite big ideas.

“Complicated” versus “complex”

Finite games are complicated.

Complicated systems require interaction with autonomous agents whose specific behaviour is beyond the observer’s control, and might be intended to defeat the observer’s objective, but whose range of behaviour is deterministic, rule-bound and known and can be predicted in advance, and where the observer’s observing behaviour does not itself interfere with the essential equilibrium of the system.

You know you have a complicated system when it cleaves to a comprehensive set of axioms and rules, and thus it is a matter of making sure that the proper models are being used for the situation at hand. Chess and Alpha Go are complicated, but not complex, systems. So are most sports. You can “force-solve” them, at least in theory.

Complicated systems benefit from skilled management and some expertise to operate: a good chess player will do better than a poor one, and clearly a skilled, fit footballer can execute a plan better than a wheezy novice — but in the right hands and given good instructions even a mediocre player can usually manage without catastrophe. While success will be partly a function of user’s skill and expertise, a bad player with a good plan may defeat a skilled player with a bad one.

Given enough processing power, complicated systems are predictable, determinative and calculable. They’re tame, not wicked problems.

Infinite games are complex.

Complex systems present as “wicked problems”. They are dynamic, unbounded, incomplete, contradictory and constantly changing. They comprise an indefinite set of subcomponents that interact with each other and the environment in unexpected, non-linear ways. They are thus unpredictable, chaotic and “insoluble” — no algorithm can predict how they will behave in all circumstances. Probabilistic models may work passably well most of the time, but the times where statistical models fail may be exactly the times you really wish they didn’t, as Long Term Capital Management would tell you. Complex systems may comprise many other simple, complicated and indeed complex systems, but their interaction with each other will be a whole other thing. So while you may manage the simple and complicated sub-systems effectively with algorithms, checklists, and playbooks — and may manage tthe system on normal times, you remain at risk to “tail events” in abnormal circumstances. You cannot eliminate this risk: accidents in complex systems are inevitable — hence “normal”, in Charles Perrow’s argot. However well you manage a complex system it remains innately unpredictable.

“Historic” versus “prospective”

Many distinctions between finite and infinite games boil down to their historical perspective: those that look backwards, concerning themselves with what has already been established and laid down — as agreed rules, formal boundaries and limited time periods for resolution necessarily do — will tend to be finite in nature; those that are open-ended, forward looking, and indeterminate — concerned with what has yet to happen, and is necessarily unknown, are infinite.

Let me throw in some original research here: historically-focused games are fine: there is no harm and much reward to be had from a game of football, as long as everyone understands the “theatricality” of what is going on; but to apply finite, backward-looking techniques to the “resolution” of infinite scenarios — necessarily forward-looking, indeterminate problems (in that you don’t even know that there is a problem, let alone what it is) is where you will get into bother.

The ostensible similarity between normal and fat-tailed distributions, yesterday.

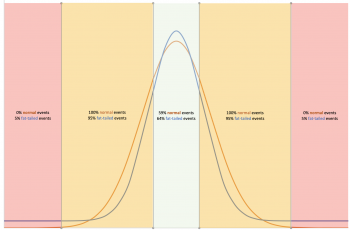
It is deceptive in that finite techniques may work perfectly well much of the time, because even infinite environments largely function by reference to established order, existing rules and what is already known: they look, for the most part, like finite games — it’s just that they don’t have to, and are liable to change without notice. As long as they behave themselves, a finite approach is efficient, effective, centrally controllable and provides consistency and certainty. This is why thought leaders are so fond of sporting metaphors.

This, we think, is just an other way of noting that the middle of a normal distribution resembles the middle of a “fat-tailed” distribution and the same approaches will work passably well for both, as long as the events fall within the middle, which for the most part they do.

“Formal” versus “substantive”

We have argued elsewhere that the great curse of modernity is the primacy of form over substance. In finite games the distinction between the two can be trivial; in an infinite game it is not.

In a backward-looking, proven, data-complete universe, substance is simply a specific articulation of form. The universe is solved; there is an exclusive optimal move and it can be derived from first principle. Substance follows from — is dependent on — form. Form is an axiom; substance is its articulation with numbers. If you have right equation — that is to say, if you follow the right form — you will get the right answer. Indeed, without the right form you have almost no chance of getting the right answer, and none at all of knowing that you have it. This depends on the universe being bounded, all rules determined, all knowns known. It depends, therefore, on the conditions existing for a finite game.

Where the universe is not bounded, where rules are unknown or changeable, where unknowns swamp knowns — where the game is infinite — substance is not a function of form. There are no equations, axioms or formulae to follow when interacting with complex adaptive systems. It will be tempting to rely on formulae that tend to work most of the time — the Black Scholes option pricing model works most of the time, at least until it does not — but this is a lazy and, at the limit, dangerous, economy. We need a different approach. Instead of the trained — those best equipped to carry out complicated instructions — we need the educated: those best equipped to observe, orient, decide and act. These people are necessarily skilled, experienced and therefore expensive.

Top-down versus bottom-up

You know, man, when I was a young man in high school
You believe it or not, I wanted to play football for the coach
And all those older guys
They said that he was mean and cruel, but you know
I wanted to play football for the coach.

Lou Reed, Coney Island Baby

Finite games tend to favour a top-down game management, with a coach and a captain. Infinite games are bottom up: every player must constantly assess her immediate environment and work out what to do based on the information she currently has.

Where form dominates, we should concentrate our resources at the centre, where we formulate rules, work out algorithms and devise playbooks, since if we get this right, success is a matter of execution, and failure comes from failure to follow the form. This has a few implications. Firstly, it means the brilliant minds belong to those at the top of the organisation: they do the most inspired thinking. Secondly, there is no more sacred quest than the creation of excellent process. Our most talented personnel are those who can write and maintain formal rules. Thirdly, those at the edges of the organisation whose job is not to formulate policy but to follow it — those who must put the leadership’s plans and algorithms into practice must not think: they must, so far as possible: quickly, flawlessly, cheaply. If you are in a finite game environment, the last thing you want them to do is make things up as they go along, as that will upset the plan. They must act like machines. The top-down model: God’s eye; the self-perpetuating autocracy.

Infinite games favour virtuoso performances in the field: in a wicked environment cheap, quick, accurate machines are no use, and the infrastructure they need to ensure they continue working may get in the way. Rather than being elaborate, internal infrastructure should be simple, robust and permissive — enabling communication, facilitating dynamic reallocation of resources, but fundamentally organising the architecture to empower quick and effective decision-making in the field. Seeing as the idea is not to win but to continue, conferring discretion upon those at the edge of the organisation who must engage with the complex adaptive system outside is not necessarily catastrophic as long as the individuals are experienced experts: they must not act like machines, and empowered — trusted to deal with unfolding situations as they perceive them. The ongoing prosperity of the organisation is an emergent property of the behaviour of these subject matter experts. This is quite the opposite model: here the greatest value is provided at the edges of the organisation. The bottom-up model: laissez-faire; invisible hand; evolutionary.

As single-round and iterated prisoner’s dilemmas

A finite game can be part of an infinite game but not vice versa. One could regard a sports franchise an an organisation playing an infinite game through the medium of finite games: here its immediate interests in each distinct match — to comprehensively, theatrically, thrash the opposition — is tempered by its wider interest to keep the infinite game going by creating a compelling sporting contest in which there is the drama that one might not, at any time, win. To carry on that wider, infinite game, one’s opponents must not only survive, but flourish to the point where they can and will beat you in a finite game, thus supplying theatre if not really drama: an unbeatable team is unsatisfying for winners, losers and spectators alike.

And here we wonder a little about the commutability of infinite games into finite ones: sporting matches are like single round prisoner’s dilemmas: zero-sum in a way that recommends only outright domination.

See also

• Paradigm failure